피너클의 it공부방
백준 13263 나무 자르기 (c++) : 피너클 본문
Convex Hull Trick 으로 풀었다.
문제를 먼저 봐보자.
만약 내가 5번 나무의 높이를 0으로 만들면 5번 보다 번호가 큰 나무를 자르기 전까지는
전기톱을 충전할때 b[5]만큼의 비용이 든다.
dp[i]는 i번째 나무를 높이가 1이 될때까지 자르는데 필요한 충전 비용의 최소값으로 정의할 것이다.
만약에 전기톱을 충전하는 비용이 100이라고 하고 나무의 높이를 10이라고 해보자.
우리는 나무를 자르고, 충전한다.
높이 10 | 충전 비용 0
높이 9 | 충전비용 100
높이 8 | 충전비용 200
높이 7 | 충전비용 300
높이 6 | 충전비용 400
높이 5 | 충전비용 500
높이 4 | 충전비용 600
높이 3 | 충전비용 700
높이 2 | 충전비용 800
높이 1 | 충전비용 900
높이 0 | 충전비용 900 + ?
이런식으로 간다. 높이가 0이되면 충전비용은 변한다.
그러니 높이를 한번에 0으로 바꾸지 않는 것이다.
dp[i]를 어떻게 계산해야 하는지 생각해보자.
먼저 현재 나무의 높이가 들어갈 것이다. 우리는 a[i] 크기의 나무를 잘라야 한다.
dp[i] = a[i]-1 // 1은 남겨야 하니 -1을 했다.
한번 자르고 한번 충전하는데는 b[0 ~ i-1] 만큼 든다.
b[i-1]이 아니라 b[0 ~ i-1] 인 이유는 1이 될때까지 잘랐기 때문이다.
j번째 나무의 높이가 0이 되었다면 그 이후 충전 비용은 b[j]일 것이다.
하지만 높이가 1이 될때까지 잘랐기 때문이 아직 충전비용은 정해지지 않았다.
dp[i] = b[0 ~ i-1] * (a[i] - 1)
이제 충전비용이 b[0 ~ i-1]이 되기 위해서는 [0 ~ i-1]번째 나무의 높이가 0이 되어야 한다.
그러기 위해서는 먼저 [0 ~ i-1]번째 나무의 높이가 1이 되어야 한다.
dp[i] = b[0 ~ i-1] * (a[i] - 1) + dp[0 ~ i-1]
그리고 나무의 높이를 0으로 만든다. 나무의 높이가 0이 되면 충전비용은 b[0 ~ i-1]이 된다.
dp[i] = b[0 ~ i-1] * (a[i] - 1) + dp[0 ~ i-1] + b[0 ~ i-1]
정리하면
dp[i] = b[0 ~ i-1] * (a[i] - 1) + dp[0 ~ i-1] + b[0 ~ i-1]
dp[i] = b[0 ~ i-1] * a[i] - 1 * b[0 ~ i-1] + dp[0 ~ i-1] + b[0 ~ i-1]
dp[i] = b[0 ~ i-1] * a[i] + dp[0 ~ i-1]
이렇게 된다.
가장 작은 값을 찾아야 하니
dp[i] = min(b[0 ~ i-1] * a[i] + dp[0 ~ i-1]) 이다.
여기서 이해가 안되는 부분이 있다.
dp[5]를 한다고 했을때 앞의 모든 나무의 높이는 1로 맞추어진 상태이다. 0이 아니다.
dp[n]을 구해도 앞의 모든 나무를 잘라야 하니 추가 계산이 필요한것이 아닐까
하지만 문제에 b[n] = 0이라고 나와있다.
즉 n번째 나무의 높이를 0으로 만들고 나면 남은 모든 나무를 자르는데 0만큼 비용이 든다.
n번째 나무를 기준으로 생각해보자.
n번째 나무를 자르는데 드는 가장 작은 비용을 찾는 것으로 해보자.
dp[n] = n번째 나무의 높이를 0으로 만드는데 드는 가장 적은 비용이다.
먼저 n번째 나무의 높이를 1로 만든다.
dp[n] = a[n]-1
나무를 자르면서 충전도 할거니 충전 비용을 곱한다.
dp[n] = b[0 ~ n-1] * (a[n] - 1)
b[0 ~ n-1]을 사용하려면 [0 ~ n-1]의 나무의 높이가 0이어야한다.
[0 ~ n-1]의 나무 높이를 1로 만들고
dp[n] = b[0 ~ n-1] * (a[n] - 1) + dp[0 ~ n-1]
0으로 만든다.
dp[n] = b[0 ~ n-1] * (a[n] - 1) + dp[0 ~ n-1] + b[0 ~ n-1]
다시 정리하면
dp[n] = b[0 ~ n-1] * a[n] + dp[0 ~ n-1] 이 된다.
다시 의문이 든다.
그냥 최대한 빨리 n번째 나무 잘라버려서 비용을 0으로 만들면 되는거 아닌가
대충 예시를 만들면
a b
1 1조
2 1
3 0
이렇게 된다.
바로 3번째 나무 높이를 0으로 만들려고 하면 1조 * 3만큼의 비용이 든다는걸 알수있고
2번째 나무 높이를 0으로 만들고 3번째 나무 높이를 0으로 만들면 1조 * 2 + 3 * 1만큼 비용이 든다는걸 알수있다.
그렇기에 우린 전부다 확인 해야한다.
이제 공식은 완성되었다.
dp[i] = min(b[0 ~ i-1] * a[i] + dp[0 ~ i-1])
이거 그냥 계산하면 n ^ 2 만큼 시간 걸린다.
그래서 Convex Hull Trick 이거를 사용한다.
j는 0 ~ i-1이라고 하면
dp[i] = min(b[0 ~ i-1] * a[i] + dp[0 ~ i-1]) 이
dp[i] = min(b[j] * a[i] + dp[j]) 이렇게 된다.
위 식에서 a[i]는 변하지 않는다.
dp[i]를 구하는 이상 a[i]는 변하지 않는다. 변하는건 j값들이다.
dp[3]를 구한다고 하면
dp[0] = min(b[0] * a[3] + dp[0])
dp[1] = min(b[1] * a[3] + dp[1])
dp[2] = min(b[2] * a[3] + dp[2])
이렇게 a[3]은 안변한다.
이제 우리는 a[i]를 x라고 생각할 것이다.
그리고 b[j]는 상수 a, dp[j]는 상수 b로 생각한다. 이렇게 되면
dp[i] = min(b[j] * a[i] + dp[j]) 이 식은
dp[i] = min(a * x + b) 이렇게 된다.
ax + b는 1차 방정식이다.
우리는 이제 그래프를 그릴수있다.
5
1 2 3 4 5
5 4 3 2 0예제 값이다. 이 값을 이용해보자.
b[] = {5, 4, 3, 2, 0}이다. 우리는 이걸 상수 a로 볼것이다.
dp[0]은 0이다. 0번째 나무는 없으니 말이다.
dp[1] = min(b[1 - 1] * a[1] + dp[1 - 1]이다. 이를 그래프로 그려보자.

대충 그렸다. 여기서 a[1]은 1이니
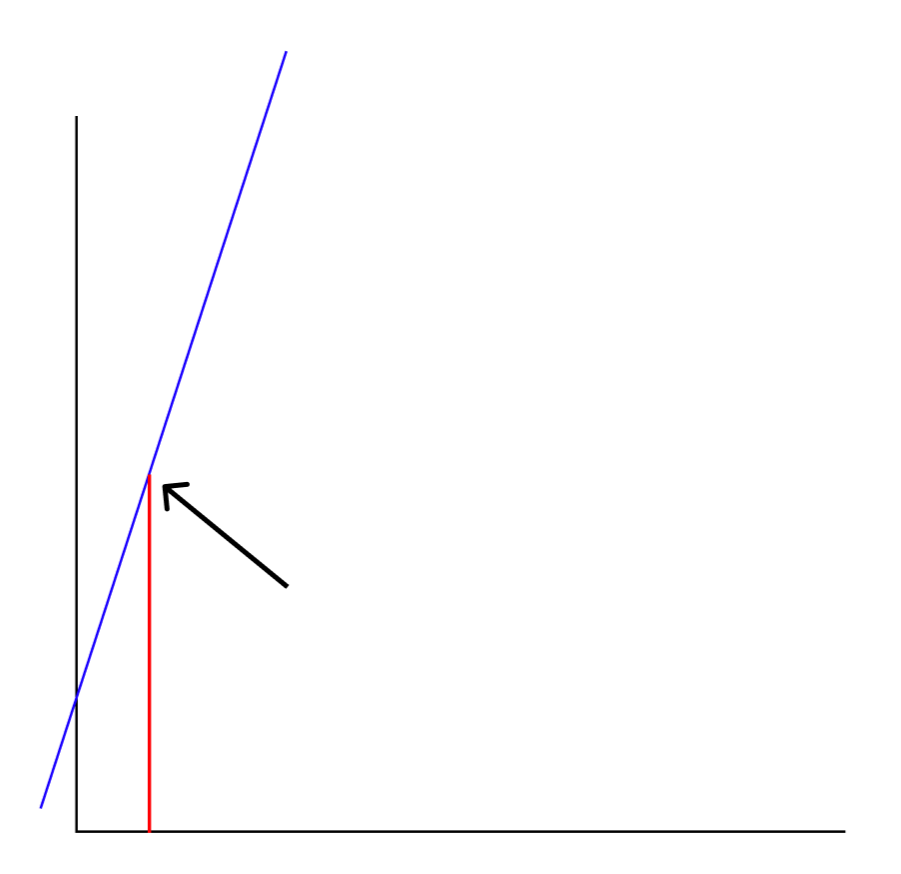
화살표 부분이 dp값이 된다.
이제 dp[2]를 그려보자.
dp[2]를 구할때는 b[2 - 1]과 dp[2 - 1]를 이용한 새로운 선이 생긴다.
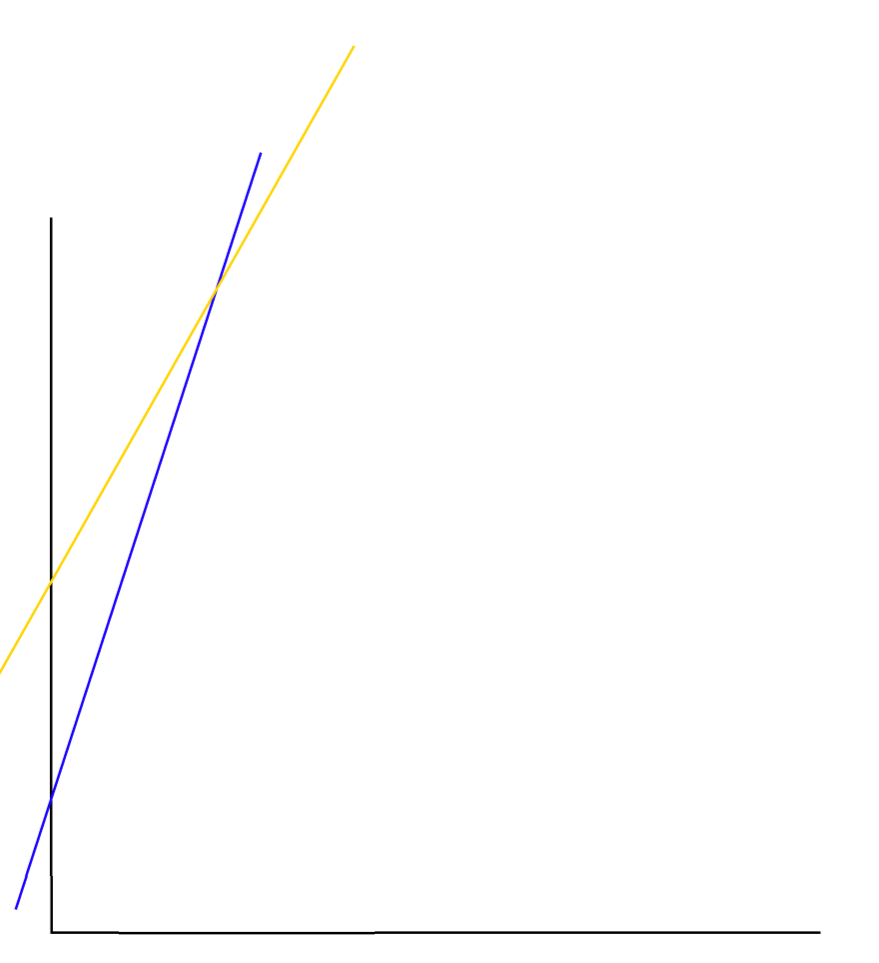
다시한번 말하지만 대충 그렸다. a[2]는 2이니 dp[2]는
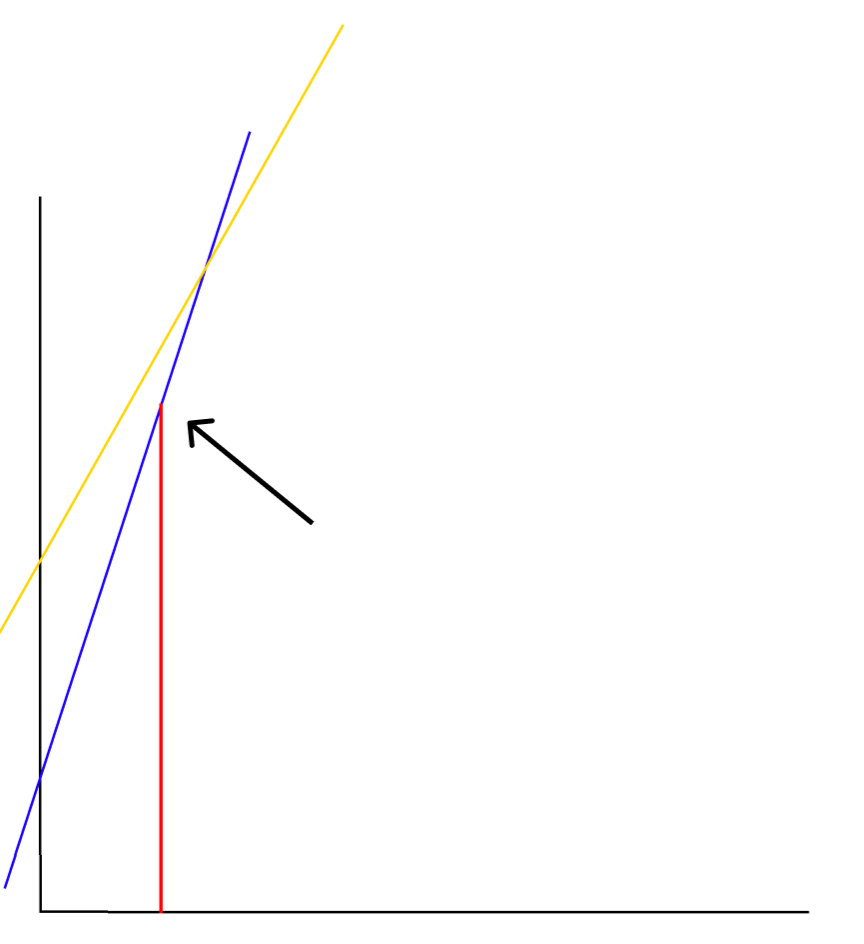
화살표로 가르키는 부분이 된다.
이젠 이걸 반복하면 된다.
우리가 할것은 선을 추가하고 a[i]를 대입했을때 값이 가장 작아지는 선분을 찾아 dp[i]안에 넣는 것이다.
여기서 조금더 나아가면 다른 생각을 할수있다.

위와 같이 선들이 있다고 생각해보자.
우리가 구하고자 하는 값은 결국 y값이다. y = ax + b이기 때문이다.
x가 주어졌을때 어느 선을 선택해야 y값이 가장 낮을까를 눈으로 보면

저 빨간 부분들이 가장 작은 y값이라는걸 알수있다.
저기 꺽이는 부분들을 보자. 선과 선이 만나면 꺽이는 부분이 생기고 더 작은 y값이 나오기 마련이다.
꺽이는 부분은 x좌표이다. y = ax + b와 y = cx + d가 만나는 부분은
ax + b = cx + d
ax - cx = d - b
(a - c)x = (d - b)
x = (d - b) / (a - c) 이다.
선과 선이 만날때마다 x좌표를 계산해서 함께 넣어주면 우리는 더욱 빠른 계산을 할수있다.
x좌표가 5일때 가장 작은 y값을 계산해야한다면 꺽이는 부분들을 모아둔 배열에서 이진 탐색을 통해 빠르게 구할수있다.
자세한 내용은 구현 부분에서 다룰것이다.
여기서 선을 추가할때 문제가 발생한다.
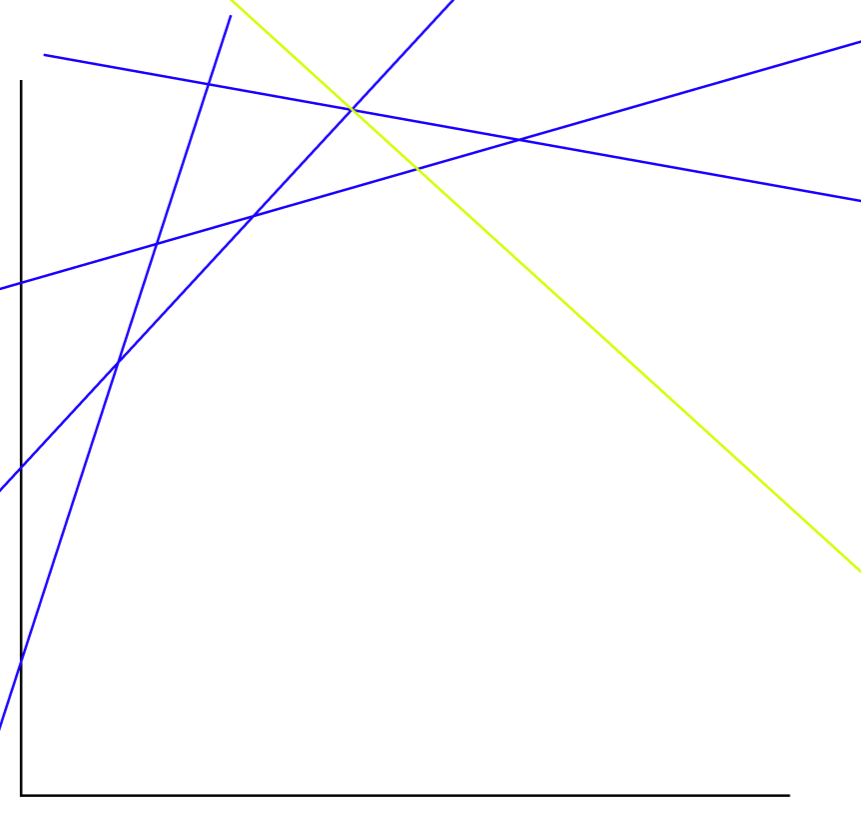
노란색의 새로운 선이 추가된다면 가장 작은 y 값들이 변하게 된다.

위 처럼 변하게 된다.
이전의 선은 필요가 없어진다. 배열 안에 들어있으면 계산을 방해하니 제거 해야한다. 어떻게 제거할수있을까?

빨간 선이 가장 늦게 추가된 선이다.
빨간 선이 갖고 있는 x 좌표는 오른쪽 화살표가 가르키고 있는 좌표이다.
오른쪽 화살표가 가르키는 x 좌표 이후에는 y좌표를 구할때 빨간 선을 이용해야한다.
하지만 새로운 선인 노란선과 빨간선이 맞닿은 x좌표는 오른 화살표 보다 왼쪽에 있다.
즉 더 작다.
노란 선은 빨간 선보다 더 낮은 x좌표에서 부터 시작해 더 낮은 y좌표를 제공한다.
결국 빨간 선은 필요가 없어진다.
우리는 빨간 선을 제거할것이다.
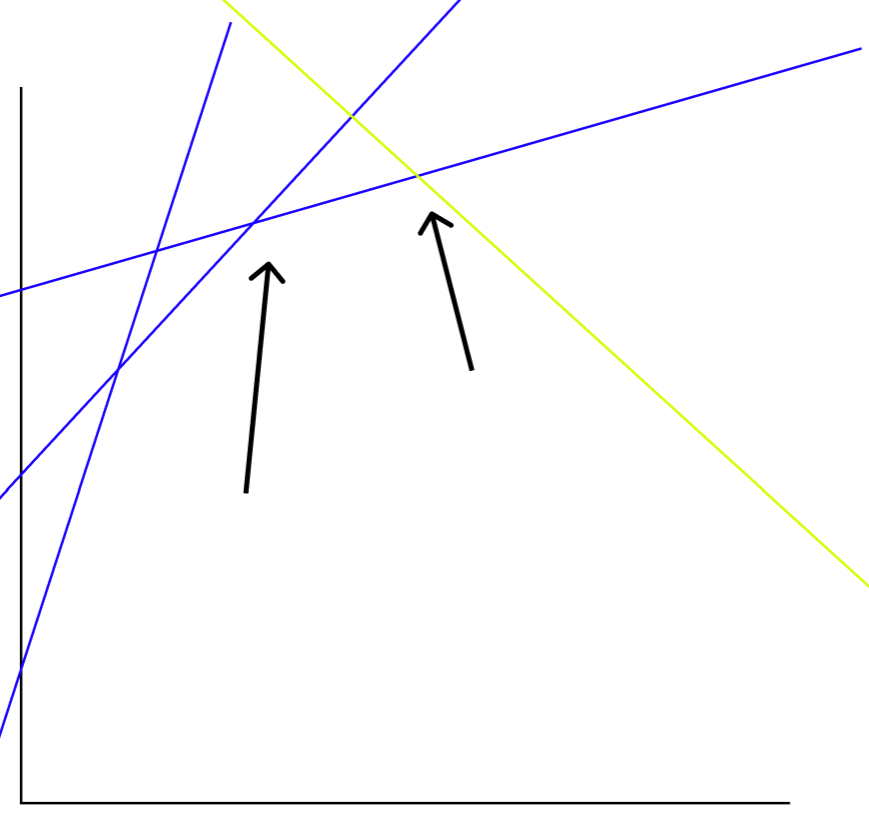
그 다음이다. 노란 선과 파란 선이 닿은 x좌표는 오른 화살표이고
기존의 파란선이 갖고있는 x좌표는 왼쪽 화살표이다.
이 선은 살아남게 되고 선을 제거하는건 여기서 그만두게된다.
이제 준비는 끝났다.
int n;
long long a[100001], b[100001];
long long dp[100001];사용할 변수들이다.
vector<tuple<long long, long long, double>> lines;위의 선들을 담을 배열이다.
제거 하기도 좋고 (pop_back) 이진 탐색에도 좋다.
tuple<a, b, x좌표> 이렇게 담겨있다.
y = ax + b에서 a와 b를 가져가고 x좌표 이후 y를 구할때 이 선을 이용한다.
tuple<5, 5, 10> 이면 y = 5x + 5이고 x=10 이후에는 y값을 구할때 이 선을 이용한다.
double get_intersection_x(tuple<long long, long long, double> a, tuple<long long, long long, double> b) {
return (double)(get<1>(a) - get<1>(b)) / (double)(get<0>(b) - get<0>(a));
}교점을 구하는 함수이다.
ax + b = cx + d
ax - cx = d - b
(a - c)x = (d - b)
x = (d - b) / (a - c) 그냥 이거다.
get<i>(tuple) 은 tuple의 i번째 값을 반환한다. get<0>(tuple<1, 2, 3) 이면 1을 반환한다.
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
for (int i = 0; i < n; i++) cin >> b[i];
dp[0] = 0;값을 입력받고 dp[0]을 0으로 만들어준다.
for (int i = 1; i < n; i++) {
// dp[i] = min(b[0 ~ i-1] * a[i] + dp[0 ~ i-1])
tuple<long long, long long, double> line_to_add = make_tuple(b[i-1], dp[i-1], 0);1부터 시작해서 n-1까지 반복한다.
line_to_add는 새로 추가할 선이다. b[i-1]과 dp[i-1]을 넣어주고 0을 채워준다.
만약 위에서 선언한 vector인 lines가 비어있다면 이 값이 그대로 들어가게된다.
그럼 x=0부터 이 선을 이용하게 되는 것이다.
while (!lines.empty()) {
tuple<long long, long long, double> top_line = lines.back();
double intersection_x = get_intersection_x(line_to_add, top_line);
if (intersection_x < get<2>(top_line)) lines.pop_back();
else break;
}선을 제거하는 부분이다.
lines는 위에서 선언한 vector로 선들이 들어간다.
top_line은 가장 최근에 vector로 들어간 선이다.
intersection_x는 가장 최근에 들어간 선과 새로 추가할 선의 교점이다. (만나는 x좌표)
만약 이 교점이 가장 최근데 들어간 선의 x좌표보다 작다면 가장 최근에 들어간 선을 제거하고
아니면 whlie문에서 나간다.

가장 최근에 추가한 선이 갖고 있는 x좌표 보다
가장 최근에 추가한 선과 새로 추가할 선과의 교점인 x좌표가 작다면 제거하고

아니면 while문에서 나간다.
if (!lines.empty()) {
tuple<long long, long long, double> top_line = lines.back();
double intersection_x = get_intersection_x(line_to_add, top_line);
line_to_add = make_tuple(get<0>(line_to_add), get<1>(line_to_add), intersection_x);
}
lines.push_back(line_to_add);만약 lines가 텅 비었다면 바로 새로 추가할 선을 추가하면 된다. 그것이 아니라면 해야할 일이 있다.
현재 line_to_add가 갖고 있는 x좌표는 0이다. 이를 가장 최근에 추가한 선과 새로 추가할 선의 교점으로 교체해줘야한다.
그것이 위에 if(!lines.empty) 부분이다.
교점 구한다음에 line_to_add에 넣어주면 된다. 맨 마지막에 intersection_x가 들어간걸 볼수있다.
long long x = a[i];
int idx = lines.size()-1;
int left = 0, right = lines.size() - 1;이제 y값, 즉 dp값을 구할것이다.
y = ax + b에서 x는 a[i], 나무의 높이가 담당한다.
idx는 lines에서 어느 선을 사용할지이다.
left와 right는 이진 탐색을 위해 준비한다.
while (left <= right) {
int mid = (left + right) / 2;
if (get<2>(lines[mid]) <= x) {
idx = mid;
left = mid + 1;
}
else {
right = mid - 1;
}
}이진 탐색이다.
lines[mid]의 x좌표가 a[i]보다 작다면 idx를 mid로 바꾸고 범위를 좁힌다.
lines[mid]의 x좌표가 a[i]보다 더 크면 안된다.
dp[i] = get<0>(lines[idx]) * x + get<1>(lines[idx]);
}
cout << dp[n-1] << '\n';
return 0;
}계산이 완료되면 y = ax + b를 계산해준다.
이렇게 하면 dp가 완료된다.
#include <iostream>
#include <algorithm>
#include <vector>
#include <tuple>
#include <stack>
using namespace std;
int n;
long long a[100001], b[100001];
long long dp[100001];
vector<tuple<long long, long long, double>> lines;
double get_intersection_x(tuple<long long, long long, double> a, tuple<long long, long long, double> b) {
return (double)(get<1>(a) - get<1>(b)) / (double)(get<0>(b) - get<0>(a));
}
int main(int argc, char** argv)
{
std::ios_base::sync_with_stdio(false);
std::cin.tie(NULL);
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
for (int i = 0; i < n; i++) cin >> b[i];
dp[0] = 0;
for (int i = 1; i < n; i++) {
// dp[i] = min(b[0 ~ i-1] * a[i] + dp[0 ~ i-1])
tuple<long long, long long, double> line_to_add = make_tuple(b[i-1], dp[i-1], 0);
while (!lines.empty()) {
tuple<long long, long long, double> top_line = lines.back();
double intersection_x = get_intersection_x(line_to_add, top_line);
if (intersection_x < get<2>(top_line)) lines.pop_back();
else break;
}
if (!lines.empty()) {
tuple<long long, long long, double> top_line = lines.back();
double intersection_x = get_intersection_x(line_to_add, top_line);
line_to_add = make_tuple(get<0>(line_to_add), get<1>(line_to_add), intersection_x);
}
lines.push_back(line_to_add);
long long x = a[i];
int idx = lines.size()-1;
int left = 0, right = lines.size() - 1;
while (left <= right) {
int mid = (left + right) / 2;
if (get<2>(lines[mid]) <= x) {
idx = mid;
left = mid + 1;
}
else {
right = mid - 1;
}
}
dp[i] = get<0>(lines[idx]) * x + get<1>(lines[idx]);
}
cout << dp[n-1] << '\n';
return 0;
}전체코드다.
'백준' 카테고리의 다른 글
| 백준 11280 2-SAT - 3 (c++) : 피너클 (5) | 2025.07.30 |
|---|---|
| 백준 4008 특공대 (c++) : 피너클 (2) | 2025.07.28 |
| 백준 2295 세 수의 합 (c++) : 피너클 (0) | 2024.11.28 |
| 백준 7785 회사에 있는 사람 (c++) : 피너클 (0) | 2024.11.26 |
| 백준 9506 약수들의 합 (c+++) : 피너클 (0) | 2024.11.24 |

