피너클의 it공부방
백준 11266 단절점 (c++) : 피너클 본문
https://www.acmicpc.net/problem/11266
단절점을 어떻게 구해야할까

위에서 단절점은 어디어디일까. 이제와서 보니 2가 두갠데 하나는 3이다.

위의 3개이다. 그럼 저것들은 왜 단절점일까?
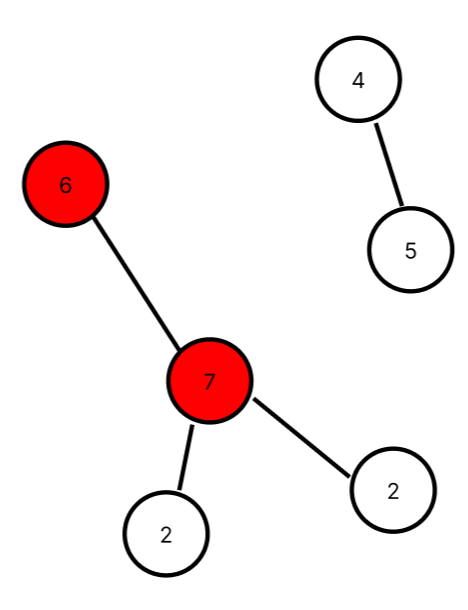
1을 제거하면 위처럼 그래프들이 처음 상태에서 떨어지게된다. connected component가 늘어나는 것이다.
6과 7도 마찮가지로 제거하면 CC가 늘어난다. 그럼 이제
제거하면 CC가 늘어나는 정점을 어떻게 구해야할까
1에서 dfs를 시작해서 6으로 향했다고 해보자
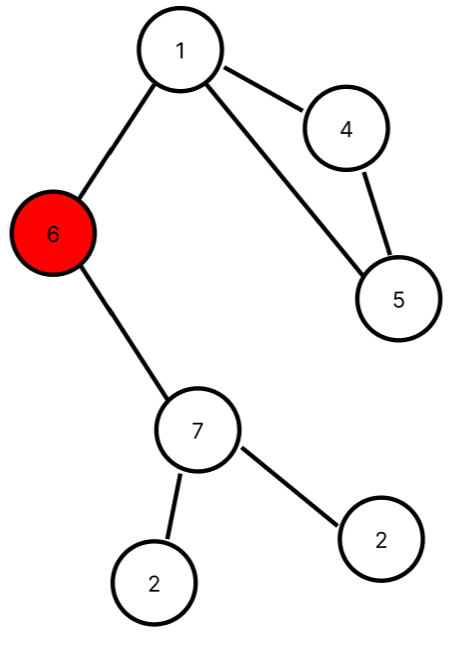
6의 자식들은 6을 제거했을때 6보다 위에있는 정점으로 연결되지 않는다. 그렇기 때문에 6을 단절점이다.
그럼 4로 가보자
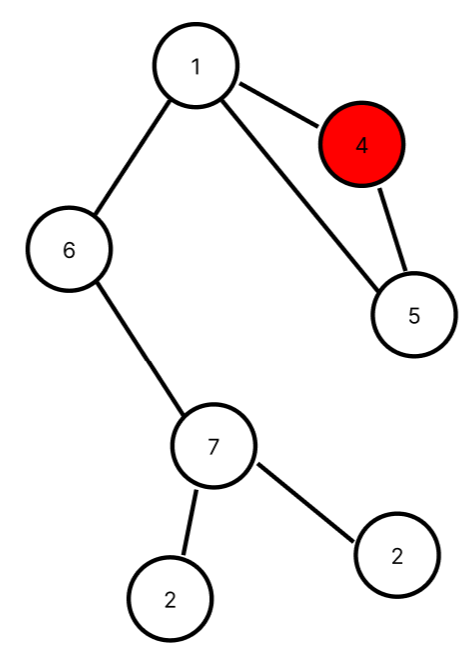
4보다 아래있는 5는 4보다 위에있는 1로 향할수가 있다. 그러니 4는 단절점이 아니다.
그럼 2와 2는 어떻게 될까? 다시한번 말하지만 둘중 하나는 3이다. 3으로 해야하는데 2로 오타냈다.
2를 제거한다고 해서 connected component는 늘어나지 않는다. 그러니 맨 끝의 정점은 단절점이 절대로 될 수 없다.
위의 과정에 있어서 가장 중요한건 '위에 있다' 라는 것이다. '위에있다'라는건 어떻게 구해야할까
void dfs(int now, int p) {
dt[now] = low[now] = ++timer;
int child = 0;이제부터 방문순서가 낮은것이 위에있는 것이다. 방문순서가 0이면 방문순서가 5인 것보다 위에있는 것이다.
이제 또 하나를 더 생각해야한다.

루트노드는 어떻게 해야할까
루트노드는 자식이 2개 이상이면 단절점이다. 위 그래프는 자식이 2개 이상이니 단절점이다.
여기서 또 한가지 자식의 개수를 어떻게 셀까
for (int i = 0; i < graph[now].size(); i++) {
int next = graph[now][i];
if (next == p) continue;
if (dt[next] == 0) {
dfs(next, now);
child++;아직 방문하지 않은 자식의 수만 셀것이다.

위 그래프에서는 1을 제거해도 connected component가 늘어나지 않는다.
6 -> 7 -> 4 -> 5 이렇게 하나로 이어지기 때문이다.
이제 준비는 끝났다.
int v, e;
vector<int> graph[10001];
int dt[10001];
int low[10001];
int timer = 0;
int ans[10001], s = 0;사용할 변수들이다.
graph는 당연히 그래프 만들때 사용할것이고
dt는 discover_time을 줄여서 만들었다. 처음 정점에 도달한 순간에 업데이트 할것이다.
low는 해당 정점이 연결되어있는 가장 위에있는 정점이 들어간다. 중요한건 0이 10보다 위에 있다는 것이다.
timer는 방문 순서에 이용할것이고
ans는 ans[i]가 1이면 단절점이라는 의미이다. s는 ans의 크기다. s=5라면 5개의 단절점이 있다는 뜻이다.
cin >> v >> e;
for (int i = 0; i < e; i++) {
int a, b;
cin >> a >> b;
graph[a].push_back(b);
graph[b].push_back(a);
}입력 받아주고
for (int i = 1; i <= v; i++) if (dt[i] == 0) dfs(i, 0);모든 정점을 확인해준다. 라고 적혀있다.
문제에 입력으로 주어지는 그래프가 연결 그래프가 아닐수도 있다고 적혀있다.
void dfs(int now, int p) {
dt[now] = low[now] = ++timer;
int child = 0;dfs함수이다.
now는 현재 정점이고 p는 부모 정점이다. p가 0이면 해당 정점이 루트라는 의미이다.
dt와 low를 둘다 timer로 초기화 해준다.
dt[5] = 5, low[5] = 5라면 5에 도착한 순서가 5번째라는 의미이다.
chlid는 당연히 처음에는 0이다.
for (int i = 0; i < graph[now].size(); i++) {
int next = graph[now][i];
if (next == p) continue;정점과 연결된 만큼 반복문을 돌려주고 만약 다음 정점이 p와 같다면 부모라는 의미이니 건너뛴다.
if (dt[next] == 0) {
dfs(next, now);
child++;dt[next]가 0이라면 아직 방문하지 않았다는 의미이다. 그러니 dfs를 바로 돌려주고 child는 1을 더해준다.

위 그래프에서 1의 자식이 2 이상이 되지 않는 이유이다.
6 -> 7 -> 5 -> 4이렇게 dfs로 이어지니 child가 두번 ++되지 않는다.
if (p == 0 && child > 1) {
if (ans[now] == 0) s++;
ans[now] = 1;
}만약 p가 0이고 (지금 정점이 루트 정점이고) child가 1보다 크다면 (자식이 2명 이상이라면) ans에 추가해준다.
else if (p != 0 && low[next] >= dt[now]) {
if (ans[now] == 0) s++;
ans[now] = 1;
}만약 p가 0이 아니고 (지금 정점이 루트 정점이 아니고) low[next]가 dt[now]보다 크거나 같다면 ans에 추가해준다.

위의 그래프에서 1 -> 6 -> 7 이 순서로 간다고 생각해보자
dt[1] = low[1] = 1;
dt[6] = low[6] = 2;
dt[7] = low[7] = 3;
일단 이렇게 초기화가 된다.
low[6] 은 dt[1]보다 크다. 그러니 6은 단절점이다. low[7]은 dt[6]보다 크다. 그러니 7은 단절점이다.
그럼 이제 1 -> 4 -> 5 이 순서로 가보자.

dt[1] = low[1] = 1;
dt[4] = low[4] = 2;
dt[5] = low[5] = 3;
일단은 이렇게 초기화가 된다.
하지만
if (dt[next] == 0) {
dfs(next, now);
child++;
if (p == 0 && child > 1) {
if (ans[now] == 0) s++;
ans[now] = 1;
}
else if (p != 0 && low[next] >= dt[now]) {
if (ans[now] == 0) s++;
ans[now] = 1;
}
low[now] = min(low[now], low[next]);
}
else {
low[now] = min(low[now], dt[next]);
}매 순간 low[now]를 업데이트 해준다.
dt[1] = low[1] = 1;
dt[4] = low[4] = 2;
dt[5] = low[5] = 3; 이렇게 되어있지만 5는 1과 연결되어있으니 당연히 1에도 접근한다.
dt[1]은 1이다. 0이 아니다. 그러니 위의 코드에서
else {
low[now] = min(low[now], dt[next]);
}이게 작동하며 low[5] = min(low[5], dt[1])이 작동한다. 결국 low[5] = 1이 된다.
dt[5] = 3, low[5] = 1인 상황이다.
for (int i = 0; i < graph[now].size(); i++) {
int next = graph[now][i];
if (next == p) continue;
if (dt[next] == 0) {
dfs(next, now);
child++;여기로 돌아가보자.
if (dt[5] == 0) {
dfs(5, 4);
child++;이렇게 바꾸면 더 보기 편하다.
현재 정점은 4이고 dt[5]는 비어있으니 dfs(5, 4)를 실행시켰다.
dt[5] = 3, low[5] = 1이 완성되었다.
if (dt[next] == 0) {
dfs(next, now);
child++;
if (p == 0 && child > 1) {
if (ans[now] == 0) s++;
ans[now] = 1;
}
else if (p != 0 && low[next] >= dt[now]) {
if (ans[now] == 0) s++;
ans[now] = 1;
}
low[now] = min(low[now], low[next]);위에서
else if (p != 0 && low[next] >= dt[now]) {
if (ans[now] == 0) s++;
ans[now] = 1;
}이 부분이 작동할때
(low[5] >= dt[4])
-> (1 >= 2) 이렇게 된다. 결국 조건문은 작동하지 않게된다.
이를 통해 우리는

위에서 1, 4, 5 부분을 제대로 구할수 있게 된다.
cout << s << '\n';
for (int i = 1; i <= v; i++) if (ans[i] == 1) cout << i << ' ';마무리로 출력만 해주면 된다.
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int v, e;
vector<int> graph[10001];
int dt[10001];
int low[10001];
int timer = 0;
int ans[10001], s = 0;
void dfs(int now, int p) {
dt[now] = low[now] = ++timer;
int child = 0;
for (int i = 0; i < graph[now].size(); i++) {
int next = graph[now][i];
if (next == p) continue;
if (dt[next] == 0) {
dfs(next, now);
child++;
if (p == 0 && child > 1) {
if (ans[now] == 0) s++;
ans[now] = 1;
}
else if (p != 0 && low[next] >= dt[now]) {
if (ans[now] == 0) s++;
ans[now] = 1;
}
low[now] = min(low[now], low[next]);
}
else {
low[now] = min(low[now], dt[next]);
}
}
}
int main(int argc, char** argv)
{
std::ios_base::sync_with_stdio(false);
std::cin.tie(NULL);
cin >> v >> e;
for (int i = 0; i < e; i++) {
int a, b;
cin >> a >> b;
graph[a].push_back(b);
graph[b].push_back(a);
}
for (int i = 1; i <= v; i++) if (dt[i] == 0) dfs(i, 0);
cout << s << '\n';
for (int i = 1; i <= v; i++) if (ans[i] == 1) cout << i << ' ';
return 0;
}
전체코드다.
'백준' 카테고리의 다른 글
| 백준 11376 열혈강호 2 (c++) : 피너클 (1) | 2025.08.14 |
|---|---|
| 백준 3006 터보소트 (c++) : 피너 (3) | 2025.08.12 |
| 백준 11280 2-SAT - 3 (c++) : 피너클 (5) | 2025.07.30 |
| 백준 4008 특공대 (c++) : 피너클 (2) | 2025.07.28 |
| 백준 13263 나무 자르기 (c++) : 피너클 (4) | 2025.07.27 |

